Некоторые темы программы по Финансовому Менеджменту, такие как «объяснять и применять основные инструменты денежного рынка» (подраздел B3) и «методы хеджирования валютного риска» и «методы хеджирования процентного риска» (раздел G) требуют либо расчет годовой эквивалентной ставки, либо расчет ставки за определенный краткосрочной период на пропорциональной основе. Существует два альтернативных способа выполнения таких расчетов, и выбор способа может оказать влияние на результаты в рамках каждой из указанных выше теме программы Финансового Менеджмента Management syllabus. Цель этой статьи – объяснить оба подхода и подчеркнуть подход, который является предпочтительным с точки зрения ACCA.
ПРИМЕР 1
Данный вопрос был опубликован в отчете экзаменатора по результатам сессии в июне 2019 года.
Публичная компания собирается заключить договор продажи с обратной покупкой на денежном рынке.
Компания согласовала продажу $10 млн. казначейских облигаций за $9.6 млн. и их последующий обратный выкуп через 50 дней за $9.65 млн.
Предположите, что в году 365 дней.
Чему равна вмененная процентная ставка по сделке, которую согласовала Компания (с округлением до 0.01%)?
Ниде представлены альтернативные способы решения задачи:
МЕТОД 1
Если требуется расчет эквивалентной ставки за определенный период, то годовую ставку следует умножить на долю года. Если требуется расчет годовой эквивалентной ставки, то ставку за определенный период следует умножить на количество периодов в году. Для таких расчетов можно использовать количество дней, либо количество месяцев в зависимости от информации, представленной в вопросе.
Ниже представлен расчет по методу 1:
Увеличение стоимости = $9.65 млн. – $9.6 млн. = $0.05 млн.
Увеличение стоимости в процентах от изначальной цены продажи = $0.05 млн./$9.6 млн. = 0.52%
Годовая эквивалентная ставка = 0.52% x 365/50 = 3.80%.
Расчет годовой эквивалентной ставки был выполнен путем умножения ставки периода на количество дней в году и деления на количество дней за период, представленный в вопросе. Если использовать количество месяцев, то ставку периода следовало бы умножить на количество месяцев в году и разделить на количество месяцев в периоде, представленном в вопросе. То есть для пятимесячного периода используется коэффициент 12/5.
Если использовать аналогичный подход для расчета ставки периода, то, например, чтобы определить ставку за три месяца, годовую ставку необходимо умножить на 3/12.
МЕТОД 2
Исходная процентная ставка возводится в степень, которая равна доле исходного периода или количеству исходных периодов в году. Здесь также можно использовать как количество дней, так и количество месяцев.
Ниже представлены расчеты примера 1 с использованием метода 2:
Увеличение стоимости = $9.65m – $9.6m = $0.05m
Увеличение стоимости в процентах от изначальной цены продажи = $0.05m/$9.6m = 0.52%
Годовая эквивалентная ставка = (1 + 0.0052) ^ (365/50) - 1 = 3.86%.
Команда экзаменатора рекомендует использовать метод 1, так как он проще и требует меньше времени, чем метод 2. Метод 1 пользуется большей популярностью при обучении и применяется в утвержденных материалах для подготовки к Финансовому Менеджменту. В особенности это касается вопросов по хеджированию валютного риска и хеджирования денежного рынка. .
ПРИМЕР 2
Следующий вопрос рассматривает хеджирование денежного рынка. Ниже представлена информация по вопросу Marigold, который был опубликован в отчете экзаменатора по результатам сессии Сен/Дек 2020:
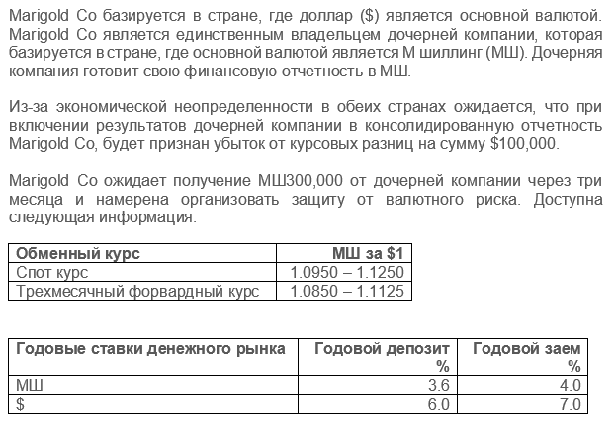

При использовании метода 1 расчеты будут выглядеть так:
Трехмесячная ставка по займу = 4% x 3/12 = 1%
Сумма, которую следует занять = MS300,000 / 1.01 = MS297,030
Сумма, которую следует разместить на депозите = MS297,030 / MS1.1250 = $264,027
Ответы на все вопросы по Финансовому Менеджменту, связанные с подобными расчетами, будут оцениваться, исходя из использования кандидатами метода 1.
Статья написана членом команды экзаменатора по Финансовому Менеджменту


