Inventory control features in the syllabuses of several ACCA exams. The areas usually tested in these exams are:
The basis of the theoretical calculations of an EOQ and an optimal ROL is that there are advantages and disadvantages of holding inventory (of buying inventory in large or small quantities). The advantages include:
The disadvantages include:
The aim behind the calculations of EOQ and ROL is to weigh up these; and other advantages and disadvantages and to find a suitable compromise level.
When determining how much to order at a time, an organisation will recognise that:
The total of annual holding and re-order costs first decreases, then increases. The point at which cost is minimised is the EOQ. This cost behaviour is illustrated by the graph in Figure 1.
Figure 1
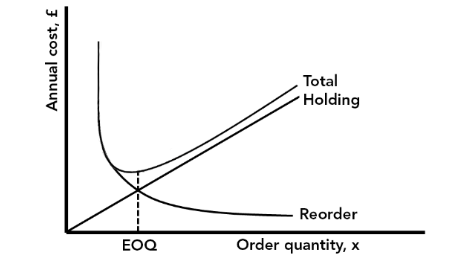
The way in which this EOQ is calculated is based on certain assumptions, including:
The assumptions result in a pattern of inventory that can be illustrated graphically as shown in Figure 2.
Figure 2
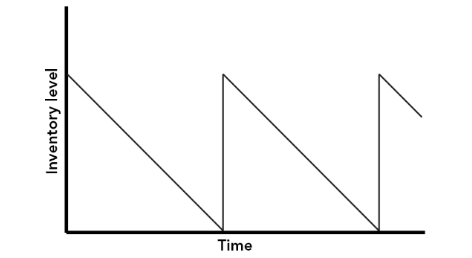
The formula
Using the standard ACCA notation in which:
CH = cost of holding a unit of inventory for a year
CO = cost of placing an order
D = annual demand
also:
TOC = total annual re-ordering cost
THC = total annual holding cost
Q = order quantity
then:
average inventory = Q/2
THC = Q/2 × CH
and:
number of orders in a year = D/Q
TOC = D/Q × CO
The total annual cost (affected by order quantity) is:
C = THC + TOC = Q/2 × CH + D/Q × CO
This formula is not supplied in exams – it needs to be understood (and remembered).
The value of Q, order quantity, that minimises this total cost is the EOQ, given by an easily remembered formula:
You need to take care over which figures you put into the formula, particularly in multiple-choice questions. The areas to beware of fall into two categories:
A common twist to exam questions is to ask students to evaluate whether bulk discounts are worth taking. While prices reduce, total annual holding costs will increase if more inventory is ordered at a time, so the matter needs a little thought.
The common approach is one of trial and error. This involves finding the total annual cost (holding cost, re-ordering cost and purchasing cost) at the level indicated by the EOQ and at the level(s) where discount first becomes available.
Figure 3 shows total costs (now including cost of purchasing the inventory) plotted against order quantity with discount incorporated.
Figure 3
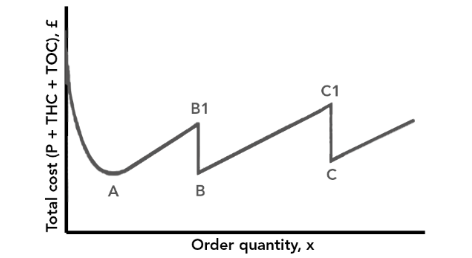
Point A represents the cost at the order quantity indicated by the EOQ. If inventory is ordered in larger quantities, total costs will increase to point B1, at which stage bulk discounts are available, bringing the costs down to point B. Any calculations will involve finding which cost out of A, B or C is the lowest, as Example 1 will show.
Example 1
Moore Limited uses 5,000 units of its main raw material per month. The material costs $4 per unit to buy, supplier’s delivery costs are $25 per order and internal ordering costs are $2 per order. Total annual holding costs are $1 per unit. The supplier has offered a discount of 1% if 4,000 units of the material are bought at a time.
Required:
Example 1 solutions
As important as how much to order at a time is the question of when to order more inventory. If an order is placed too late, when inventories have been allowed to run too low, a ‘stock-out’ will occur, resulting in either a loss of production or loss of sales, or possibly both.
If orders are placed too soon, when there are still substantial supplies in inventory, then inventory levels and holding costs will be unnecessarily high. The re-order level as explained below should not be confused with the inventory control levels referred to in textbooks – this article ignores these. When it comes to calculating re-order levels, three sets of circumstances can be envisaged.
‘Lead-time’ is the interval between placing an order with a supplier and that order arriving. It is unlikely that this could be reduced to zero – it would require astonishingly co-operative and efficient suppliers. If it were possible, a re-order level of zero could be adopted. An organisation could simply wait until it ran out of inventory, click its corporate fingers, and inventory would arrive instantaneously.
The assumption of constant demand is consistent with the assumptions underlying the EOQ formula. If suppliers take some time to provide goods, orders need to be placed in advance of running out. Figure 4 illustrates the problem and its solution.
Figure 4
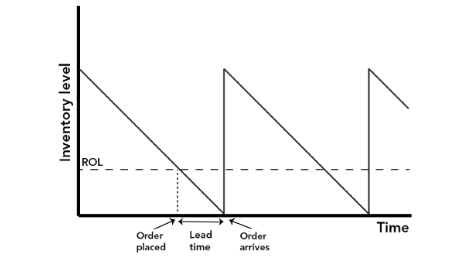
If the lead-time is, say, five days, an order has to be placed before inventories have been exhausted. Specifically, the order should be placed when there is still sufficient inventory to last five days, ie:
Re-order level (ROL) = Demand in lead-time
So, if lead-time for a particular inventory item is five days and daily demand is 30 units, the re-order level would be five days at 30 units per day, 150 units.
If demand in lead-time varied, it could be described by means of some form of probability distribution. Taking the previous example of the demand in lead-time being 150 units, we’re considering the possibility of demand being more than 150 or less than that.
Note: This aspect of inventory control produces a few problems. The EOQ formula requires that demand (and lead-time) for a inventory item be constant. Here the possibility of demand varying or lead-time varying or both varying is introduced. Setting that problem aside, most ACCA syllabuses at the lower levels avoid any discussion of uncertainty or probability distributions. However, uncertainty in lead-time demand in inventory control has featured in exams.
In these circumstances, a firm could place an order with a supplier when the inventory fell to 150 units (the average demand in the lead-time). However, there’s a 33% chance (0.23 + 0.08 + 0.02 = 0.33) that demand would exceed this re-order level, and the organisation would be left with a problem. It is therefore advisable to increase the re-order level by an amount of ‘buffer inventory’ (safety inventory).
Buffer inventory is simply the amount by which ROL exceeds average demand in lead-time. It is needed when there is uncertainty in lead-time demand to reduce the chance of running out of inventory and reduce the cost of such shortages.
If a ROL of 160 units was adopted, this would correspond to a buffer inventory of 10 units (and reduce the chance of running out of inventory to 0.08 + 0.02 = 0.1, or 10%). A ROL of 170 is equivalent to a buffer inventory of 20 and reduces the chance of running out to 2%, and a ROL of 180 implies 30 units of buffer inventory (and no chance of running short).
This leaves the problem of how to calculate the optimal ROL. There are two common ways in which one could determine a suitable re-order level (if the information was available):
Written by a member of the management accounting examining team